Modèles d'éclairement implémentés

Lors du rendu, le calcul de la couleur d'un texel s'effectue donc en appliquant un modèle d'éclairement à un point du nuage (un QLS) sélectionné par son hémisphère de visibilité. Comme une texture directionnelle stocke la visibilité des points du nuage en fonction de la direction d'observation, lors du rendu nous sélectionnons le sous ensemble des points visibles du nuage auquels nous devons appliquer le modèle d'éclairement. Le nombre de points de ce sous ensemble est toujours constant : si $d$ est la définition des textures, sachant qu'au maximum 3 faces de la boîte sont visibles à un instant donné, nous n'auront à calculer l'illumination que de $3.d²$ points.

Par exemple, dans nos tests, le nuage de points que nous utilisons est constitué en moyenne de 1.5 million de points. Pour une définition de texture de 128x128 texels, nous n'appliquons le calcul d'illumination qu'à 49512 points, soit 3% des points. Ceci nous permet d'employer des modèles d'illumination coûteux en temps de calculs tels que l'application de BRDF acquises physiquement, ou de calculer l'auto-ombrage des points.

Nous avons implémenté le modèle d'éclairement de Phong, le placage d'environnement ainsi que l'application de BRDF acquise physiquement (section 3.3.2.2). Nous avons également implémenté l'auto-ombrage avec une compression originale l'hémisphère d'ombrage des points, que nous présentons en section 3.3.2.3 et en Annexe B.

Repère local des points

Pour appliquer les différents modèles d'éclairement locaux, nous devons disposer d'un repère

Figure 3.15: Construction du repère
local d'un point.

0.40

local en chaque point permettant d'y exprimer les directions d'observation et d'éclairement. Etant donné que nous ne disposons que des coordonnées 3D du point et de sa normale, nous construisons un repère orthonormé de la façon suivante : soient $\overrightarrow{v}(\theta_{v},\varphi_{v})$ la normale à laquelle on doit associer une base et $(\overrightarrow{x},\overrightarrow{y},\overrightarrow{z})$ le repère global de la scène, on crée tout d'abord un vecteur $\overrightarrow{v_{p}}$ perpendiculaire à $\overrightarrow{v}$ par $\overrightarrow{v_{p}}=(\theta_{v},\varphi_{v}+\pi/2)$ (figure 3.15), puis le repère est finalement obtenu en ajoutant le dernier axe : $\overrightarrow{v_{B}}=\overrightarrow{v}\wedge\overrightarrow{v_{p}}$ . Les cas particuliers des pôles ( $\overrightarrow{v}$ colinéaire à $\overrightarrow{y}$) sont traités séparément.

L'intérêt de procéder ainsi, par rapport à une rotation du repère, est que dans notre implémentation, le nombre d'opérations arithmétiques à effectuer est inférieur, et comme nous devrons effectuer ce calcul pour chaque texel, les calculs doivent être rapides.

BRDF par acquisition physique

Principe

Nous avons utilisé la BRDF d'une surface réelle, acquise à l'aide d'un spectrophotogoniomètre. Le principe est d'échantillonner la BRDF d'une surface selon un nombre fixé de directions et d'utiliser directement ces données pour calculer la couleur du point en fonction de la direction d'éclairement et d'observation.

Dans nos travaux, nous avions à notre disposition deux BRDF isotropes : la BRDF du satin et une BRDF synthétique. Cette dernière est créée ''à la main'' afin de valider l'implémentation, et donne les couleurs rouge, verte ou bleue en fonction de la direction de la lumière et de l'éclairement.

Structure des données

La structure de données représentant la BRDF est un tableau $B$ à quatre dimensions représentant la réflectance de la surface dans une direction d'observation $(\theta_{o},\varphi_{o})$ en fonction de la direction d'éclairement $(\theta_{L},\varphi_{L})$ (figure 3.16(a)). Dans notre cas, la longueur d'onde de la lumière est constante, ainsi nous ne stockons que les composantes $(R,V,B)$ de la couleur en chaque élément du tableau.

Figure 3.16: BRDF par acquisition physique.

[Principe de la BRDF.][Interpolations bilinéaires des couleurs.]

Application

Pour passer d'une BRDF discrète, représentée par le tableau $B$ à quatre dimensions, à une BRDF continue sur l'hémisphère, nous interpolons bilinéairement les couleurs entre les directions discrétisées.

Par exemple, pour une direction d'observation discrétisée $\overrightarrow{V}$ et une direction d'éclairement non discrétisée $\overrightarrow{l}$, la couleur $C$ obtenue est calculée comme suit (voir figure 3.16(b)) :

Soit 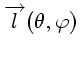$\overrightarrow{l}(\theta,\varphi)$ la direction d'éclairement, $\overrightarrow{L_{0}}$, $\overrightarrow{L_{1}}$, $\overrightarrow{L_{2}}$ et $\overrightarrow{L_{3}}$ ses directions discrétisées adjacentes, on obtient les couleurs $C_{i}$ associées aux directions d'éclairement discrétisées par $C_{i}=B[\overrightarrow{V},\overrightarrow{L_{i}}]$, $i\in[0,1,2,3]$.

Ensuite on interpole ces valeurs bilinéairement :

$$C=C_{a}+k_{\theta}.(C_{b}-C_{a})$$

$$\textrm{avec }C_{a}=C_{0}+k_{\varphi}.(C_{3}-C_{0})$$

$$\textrm{et }C_{b}=C_{1}+k_{\varphi}.(C_{2}-C_{1})$$

Symétriquement, nous appliquons ce principe pour la direction (non discrétisée) d'observation : nous calculons la couleur finale par interpolation bilinéaire des quatres couleurs issues des directions discrétisées de la direction d'observation.

Ainsi, pour obtenir une couleur en fonction d'une direction d'observation et d'éclairement quelconque, nous devons effectuer cinq interpolations bilinéaires. C'est un calcul lourd mais, comme nous le verrons dans la section des résultats, il s'effectue en temps réel sur une machine milieu de gamme (Athlon 1Ghz).

Auto-ombrage par hémisphère d'ombrage quantifié

Le principe de l'auto-ombrage est de prendre en compte, lors du rendu d'un modèle géométrique, la projection de l'ombre qu'il induit sur son propre relief, en fonction d'une source de lumière ponctuelle. L'auto-ombrage ajoute beaucoup de réalisme au rendu, mais est également coûteux à calculer.

Parmi les techniques existantes à notre disposition, qui fonctionnent en temps réel, la méthode présentée par Williams [Wil78] permet de calculer cet auto-ombrage si l'on dispose au moment du rendu du maillage géométrique de la scène, ce qui n'est pas notre cas. Dans le cas ou le relief du modèle est représenté par des cartes d'élévation, les techniques d'horizon-mapping [Max88,SC00,HS99] (voir section 1.4.1.3) peuvent être employées, mais nos textures plaquées sur la boîte englobante ne sont pas exprimables sous forme de champ de hauteur : le relief peut varier complètement d'un point de vue à l'autre.

En Annexe B, nous présentons le principe de notre décomposition en harmoniques principaux de l'hémisphère d'ombrage que nous avons développé.

Le principe est de créer, pour un point donné, son hémisphère d'ombrage (voir la section 1.4.1.3 page ). L'ensemble des directions de l'hémisphère est discrétisé en coordonnées sphériques de façon habituelle et stocke en chaque direction $(\alpha,\beta)$, correspondant à la direction de la lumière, la valeur 0 si le point est dans l'ombre, ou la valeur 1 dans le cas contraire.

Ensuite, la fonction d'ombrage $f(\alpha,\beta)$ (voir Annexe B) définie à partir de cet hémisphère est décomposée en harmoniques principaux avec la transformée de Fourier 2D discrète de $f$. Les harmoniques sont quantifiés et stockés sur 9 octets.

Ces harmoniques nous permettent, lors du rendu, de reconstruire l'hémisphère d'ombrage avec la transformée de Fourier inverse, ce qui s'avère très rapide : quelques cosinus à calculer (voir Annexe B).

La fonction d'ombrage obtenue prenant ses valeurs dans l'intervalle $[0,1]$, nous appliquons ce coefficient à la couleur calculée par le modèle d'éclairement du point.

Durant la phase de précalculs, nous obtenons l'hémisphère d'ombrage d'un point avec un lancer de rayons dans la scène complexe d'origine, selon toutes les directions discrétisées de l'hémisphère. Dans nos tests nous avons discrétisé l'hémisphère selon 16 azimuths et 8 angles d'élévation, soit 129 directions. Nous avons expérimenté une discrétisation plus fine (513 directions) sans noter de différence visuelle significative dans la précision des ombres.