Acquisition d'une texture directionnelle
La différence principale avec la méthode précédente est que nous ne nous basons plus sur un lancer de rayon pour précalculer l'hémisphère des directions en chaque texel. A la place, nous projetons le nuage de points issu du modèle complexe sur chaque plan de la boîte.
Tout d'abord, nous devons transformer le maillage de l'objet de base en un nuage dense de points.
Décomposition en surfels du modèle complexe
Ce nuage de points est obtenu à partir du maillage de triangles du modèle complexe. L'algorithme consiste à subdiviser récursivement chaque triangle comme suit.
Étant donné un triangle ![]() , nous le subdivisons en 4 en scindant
ses arêtes en deux, comme le montre la figure 3.10.
Ensuite, nous appliquons la subdivision aux sous-triangles créés.
Le critère d'arrêt est le suivant : nous ne subdivisons pas les triangles
constitués d'une arête plus petite qu'une distance fixée. Cette technique
n'est pas optimale dans le cas de triangles très étirés, car la subdivision
se termine en fonction de la plus petite de ses arêtes. Néanmoins,
dans le cas où le maillage est constitué de triangles ''raisonnablement''
proportionnés, la méthode fonctionne bien.
, nous le subdivisons en 4 en scindant
ses arêtes en deux, comme le montre la figure 3.10.
Ensuite, nous appliquons la subdivision aux sous-triangles créés.
Le critère d'arrêt est le suivant : nous ne subdivisons pas les triangles
constitués d'une arête plus petite qu'une distance fixée. Cette technique
n'est pas optimale dans le cas de triangles très étirés, car la subdivision
se termine en fonction de la plus petite de ses arêtes. Néanmoins,
dans le cas où le maillage est constitué de triangles ''raisonnablement''
proportionnés, la méthode fonctionne bien.
![\includegraphics[%
width=0.90\columnwidth,
keepaspectratio]{eps/tdpv-subdivision.eps}](img369.png)
|
L'ensemble de points que nous obtenons avec cet algorithme est défini par tous les sommets des triangles subdivisés (figure 3.10(d)). Chaque point est défini par ses coordonnées 3D dans le repère de la scène ainsi que par sa couleur et sa normale. Ces données sont interpolées lors de la subdivision à partir des sommets du maillage de base.
La figure 3.11 montre le résultat de cet algorithme appliqué à deux modèles géométriques.
![\includegraphics[%
width=1.0\columnwidth,
height=5cm,
keepaspectratio]{eps/tdpv-tore-points.eps}](img370.png) ![\includegraphics[%
width=1.0\columnwidth,
height=5cm,
keepaspectratio]{eps/tdpv-torus.eps}](img371.png)
|
Une fois ce nuage de points créé, nous calculons les textures directionnelles appliquées à la boîte englobante.
Calcul de la texture
Comme pour la méthode précédente, une texture directionnelle stocke en chaque texel les points du modèle complexe s'y projetant pour toutes les directions d'un hémisphère. La différence est que nous n'effectuons pas de lancer de rayons pour obtenir ces points.
Pour chaque direction ![]() de l'hémisphère d'une face
de l'hémisphère d'une face ![]() de
la boîte, l'algorithme permettant d'obtenir une texture directionnelle
est le suivant (figure 3.12) :
de
la boîte, l'algorithme permettant d'obtenir une texture directionnelle
est le suivant (figure 3.12) :
Pour chaque direction ![]() de l'hémisphère :
de l'hémisphère :
- Créer un tampon de profondeurs
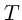 à deux dimensions, de résolution
égale à la définition de la texture, positionné sur
à deux dimensions, de résolution
égale à la définition de la texture, positionné sur 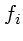 , stockant
en chaque élément
, stockant
en chaque élément 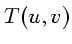 la profondeur
la profondeur  et un l'indice
et un l'indice  d'un point dans le nuage.
d'un point dans le nuage.
- Projeter orthographiquement tous les points du nuage sur
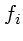 en ne gardant en chaque
en ne gardant en chaque 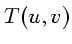 que le point le plus proche parmi
ceux qui s'y projetent.
que le point le plus proche parmi
ceux qui s'y projetent.
- Stocker l'indice
 pour la direction
pour la direction  de l'hémisphère de chaque
texel
de l'hémisphère de chaque
texel 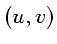 .
.
Nous obtenons finalement une texture stockant en chaque élément un tableau d'indices de points (un point par direction).
Hémisphère des directions
Par rapport à la méthode précédente, nous avons amélioré la répartition des directions. La problématique de la discrétisation de l'hémisphère est que la répartition doit :
- permettre une localisation d'un vecteur quelconque très rapidement,
- distribuer le mieux possible un nombre fixé de directions de façon à couvrir uniformément la surface de la scène.
Concernant la distribution des directions, la discrétisation régulière des directions en coordonnées sphériques donne de mauvais résultats en termes de recouvrement de la scène : comme le montre la figure 3.13, les angles rasants donnent des points trés éloignés d'une direction à l'autre, ce qui se traduit, lors du rendu, par de fortes discontinuités entre deux directions voisines.
![\includegraphics[%
width=0.80\columnwidth,
keepaspectratio]{eps/tdpv-echant-surface.eps}](img376.png)
|
Pour améliorer cette répartition, nous avons augmenté le nombre de
directions sur les angles rasants. C'est à dire qu'au lieu de subdiviser
régulièrement l'angle d'élévation ![]() , nous utilisons des intervalles
se réduisant petit à petit selon une courbe en racine carrée (cf.
figure 3.14). Cette fonction nous permet techniquement
de conserver des calculs de localisation très rapides.
, nous utilisons des intervalles
se réduisant petit à petit selon une courbe en racine carrée (cf.
figure 3.14). Cette fonction nous permet techniquement
de conserver des calculs de localisation très rapides.
![\includegraphics[%
width=1.0\columnwidth,
height=6cm,
keepaspectratio]{eps/tdpv-sqrt-bw.eps}](img378.png) ![\includegraphics[%
width=1.0\columnwidth,
height=6cm,
keepaspectratio]{eps/tdpv-regulier-adapte.eps}](img379.png)
|
Porquet Damien 2005-03-02
![\includegraphics[%
width=0.70\columnwidth,
keepaspectratio]{eps/tdpv-creation.eps}](img375.png)