Interpolation avec calcul au vol
du déplacement
Pour nous affranchir de cette dépendance vis à vis du processeur central, nous avons alors essayé de n'avoir aucune étape de calcul effectuée par le CPU, c'est à dire de délocaliser tous les calculs dans le pixel shader de la carte graphique.
Problématique
Le problème est le même que celui exposé dans la section précédente : le pixel shader ne nous permet pas d'écrire où l'on veut à l'écran. La problématique, du point de vue du shader, peut s'exprimer ainsi : ''Trouver le meilleur texel à retourner parmi les deux textures de référence, sachant que la position actuelle de rastérisation à l'écran est p(x,y).''
Réalisation
La figure 2.15 détaille le problème : il faut déterminer
la couleur du pixel ![]() du point de vue virtuel. Au début de l'interpolation
(
du point de vue virtuel. Au début de l'interpolation
(![]() ), la couleur de
), la couleur de ![]() est issue du point
est issue du point ![]() de la surface
de la scène. A la fin de l'interpolation, (
de la surface
de la scène. A la fin de l'interpolation, (![]() ), la couleur de
), la couleur de
![]() est issue de
est issue de ![]() .
. ![]() et
et ![]() sont obtenus à partir
du tampon de profondeur de chaque point de vue de référence par projection
inverse. Pour un instant intermédiaire de l'interpolation, la couleur
de
sont obtenus à partir
du tampon de profondeur de chaque point de vue de référence par projection
inverse. Pour un instant intermédiaire de l'interpolation, la couleur
de ![]() est issue de l'intersection de son rayon optique avec la surface
de la scène, c'est à dire du point
est issue de l'intersection de son rayon optique avec la surface
de la scène, c'est à dire du point ![]() , sur la partie droite
de la figure 2.15.
, sur la partie droite
de la figure 2.15.
Dans notre algorithme, nous considérons que l'intersection entre l'axe
optique de ![]() et la surface de la scène décrit un segment 3D dans
l'espace de la scène, segment qui débute en
et la surface de la scène décrit un segment 3D dans
l'espace de la scène, segment qui débute en ![]() et se termine
en
et se termine
en ![]() . Sur la partie droite de la figure, nous considérons donc
que le point d'intersection est
. Sur la partie droite de la figure, nous considérons donc
que le point d'intersection est ![]() au lieu de
au lieu de ![]() .
.
Notre algorithme consiste alors à :
- interpoler linéairement
 entre
entre  et
et  mais dans
l'espace de chaque image de référence au lieu de la scène (pour des
raisons de complexité du calcul, la taille d'un shader étant limitée).
Pour cela, comme l'illustre la figure 2.16, il
faut d'abord projeter
mais dans
l'espace de chaque image de référence au lieu de la scène (pour des
raisons de complexité du calcul, la taille d'un shader étant limitée).
Pour cela, comme l'illustre la figure 2.16, il
faut d'abord projeter  sur le plan de projection du point
de vue 0 (
sur le plan de projection du point
de vue 0 (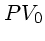 ) et
) et  sur
sur 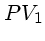 . On obtient alors les
points 2D
. On obtient alors les
points 2D  et
et  dans l'espace des l'images des
dans l'espace des l'images des
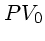 et
et 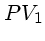 (respectivement).
(respectivement).
- Ensuite, nous calculons les points
 et
et  par interpolation
linéaire en 2D sur les segments
par interpolation
linéaire en 2D sur les segments
![$ [p,p_{1,0}]$](img285.png) et
et
![$ [p_{0,1},p]$](img286.png) ,
soit :
,
soit :
 et
et
 .
.
- Finalement, pour déterminer le meilleur point entre
 et
et
 , nous procédons comme suit :
, nous procédons comme suit :
- Nous reprojetons
 et
et  dans l'espace de la scène
(figure 2.17(a)) : on obtient les points
dans l'espace de la scène
(figure 2.17(a)) : on obtient les points  et
et 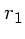 .
.
Figure 2.17: Détermination du meilleur point de vue. [Reprojection des points 2D interpolés dans l'espace de la scène.]![\includegraphics[%
width=0.48\columnwidth]{eps/exp-pv-interp-au-vol4.eps}](img290.png) [Projection des points 3D sur le plan de la caméra virtuelle.]
[Projection des points 3D sur le plan de la caméra virtuelle.]![\includegraphics[%
width=0.48\columnwidth]{eps/exp-pv-interp-au-vol5.eps}](img291.png)
- Le meilleur point de vue est celui dont le point
 est le plus
proche de
est le plus
proche de  . En pratique, pour calculer le plus proche, nous
projetons
. En pratique, pour calculer le plus proche, nous
projetons  et
et 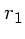 sur le plan de la caméra virtuelle
(figure 2.17(b)) : on obtient les points
sur le plan de la caméra virtuelle
(figure 2.17(b)) : on obtient les points  et
et  et nous comparons en 2D la distance
et nous comparons en 2D la distance
 avec
avec
 .
.
- Nous reprojetons
Résultats
Les premiers résultats montrèrent des problèmes au niveau des bordures de l'objet, mais une interpolation correcte dans les parties de l'image se superposant entre le point de vue 0 et le point de vue 1. La figure 2.18, montre le résultat de l'interpolation pour les points valides de l'image.
![\includegraphics[%
width=1.0\columnwidth,
height=4cm,
keepaspectratio]{eps/pm-0-1.png.eps}](img297.png) ![\includegraphics[%
width=1.0\columnwidth,
height=4cm,
keepaspectratio]{eps/pm-0-2.png.eps}](img298.png) ![\includegraphics[%
width=1.0\columnwidth,
height=4cm,
keepaspectratio]{eps/pm-0-3.png.eps}](img299.png)
|
Comme le montre la figure 2.19, le problème des
pixels en bordure de l'image est dû au fait que, pour ces pixels,
il n'existe pas de point ![]() ou
ou ![]() .
.
|
[Problème des pixels contenus dans l'image d'arrivée mais pas dans l'image de départ.]
![\includegraphics[%
width=0.30\columnwidth]{eps/exp-pv-interp-au-vol1.eps}](img300.png) [Problème des pixels contenus dans l'image de départ mais pas dans l'image de d'arrivée.] [Problème des pixels contenus dans l'image de départ mais pas dans l'image de d'arrivée.]![\includegraphics[%
width=0.30\columnwidth]{eps/exp-pv-interp-au-vol2.eps}](img301.png)
|
Pour résoudre ce problème, nous disposons une boîte englobante autour
de la scène. Celle-ci permet de générer un point dans tous les cas.
Néanmoins, nous devons prendre quelques précautions : dans le cas
(a) de la figure 2.19, nous interpolons ![]() entre
entre ![]() et
et ![]() dans la texture du
dans la texture du ![]() mais nous
ignorons le
mais nous
ignorons le ![]() car il ne peut pas donner de points pertinents
dans ce cas. Nous procédons symétriquement pour le second cas, figure
(b).
car il ne peut pas donner de points pertinents
dans ce cas. Nous procédons symétriquement pour le second cas, figure
(b).
La figure 2.20 montre le résultat de l'interpolation
avec cette amélioration. Les zones vertes correspondent au cas (b)
de la figure 2.19, et les zones bleues au cas
(a). Comme on peut le distinguer sur la queue et les pattes avant
du tigre sur la figure, à ![]() , les pixels pour lesquels on ne
dispose ni de
, les pixels pour lesquels on ne
dispose ni de ![]() ni de
ni de ![]() (les pixels noirs) ne sont pas
interpolés, ce qui donne des trous.
(les pixels noirs) ne sont pas
interpolés, ce qui donne des trous.
Ainsi, pour que cette méthode fonctionne il faut que les points de vue de départ et d'arrivée ne soient pas trop éloignés afin d'augmenter les zones de recouvrement. L'avantage est que le rendu est très rapide (>90 FPS avec une Radeon 9700), totalement indépendant de la complexité de la scène et demande peu de mémoire : une texture de couleurs par point de vue, car le tampon de profondeurs nécessaire en chaque point de vue de référence est stocké dans la composante alpha de la texture. Ainsi, un point de vue occupe environ 700Ko (avec compression DXT1) en mémoire vidéo.
![\includegraphics[%
width=0.23\columnwidth,
keepaspectratio]{eps/exp-real-0.ppm.eps}](img305.png) ![\includegraphics[%
width=0.23\columnwidth,
keepaspectratio]{eps/exp-real-2.ppm.eps}](img306.png) ![\includegraphics[%
width=0.23\columnwidth,
keepaspectratio]{eps/exp-real-1.ppm.eps}](img307.png) ![\includegraphics[%
width=0.23\columnwidth,
keepaspectratio]{eps/exp-real-3.ppm.eps}](img308.png)
|
Nous avons également testé la méthode avec un modèle de 871000 faces.
Nous avons observé des déformations au sein des parties de l'image
recouvertes par les deux points de vues. Ces déformations sont dûes
au fait que la surface entre les points ![]() et
et ![]() est supposée
plate, ce qui n'est que rarement le cas. La ligne supérieure de la
figure 2.21 montre les points réellement
balayés par le rayon optique issu d'un pixel de la caméra virtuelle,
et la ligne du bas montre les points que nous balayons avec notre
méthode. L'approximation est bonne dans certains cas : la premiere
colonne d'images par exemple. Mais dans le cas général (les autre
images), notre approximation linéaire est fausse.
est supposée
plate, ce qui n'est que rarement le cas. La ligne supérieure de la
figure 2.21 montre les points réellement
balayés par le rayon optique issu d'un pixel de la caméra virtuelle,
et la ligne du bas montre les points que nous balayons avec notre
méthode. L'approximation est bonne dans certains cas : la premiere
colonne d'images par exemple. Mais dans le cas général (les autre
images), notre approximation linéaire est fausse.
Ceci nous empêche d'utiliser cette méthode à grande échelle, c'est à dire pour un relief quelconque et des points de vue de référence éloignés.
Discussion
L'interpolation de points de vue par pixel s'avère difficile à employer dans le cadre d'une application complète de réalité virtuelle. Dans l'implémentation la plus convaincante visuellement (section 2.3.2), le problème est le trop grand temps de calcul nécessaire. Dans l'implémentation accélérée que nous avons développée (section précédente), nous n'avons pas réussi à prendre en compte l'intégralité des pixels si les points de vue de références sont trop éloignés (voir la figure 2.20). Dans ce cas, la restriction la plus importante que nous avons est que les points de vues de départ et d'arrivée doivent être très proches pour que la méthode fonctionne correctement. Malgré tout, le principe du calcul par pixel s'avère extrêmement rapide, en dépit des lourdes opérations de calcul matriciel effectuées pour chaque pixel affiché.
Porquet Damien 2005-03-02
![\includegraphics[%
width=0.80\columnwidth]{eps/exp-pv-interp-au-vol0.eps}](img279.png)
![\includegraphics[%
width=0.85\columnwidth]{eps/exp-pv-interp-au-vol3.eps}](img282.png)
![\includegraphics[%
width=1.0\columnwidth,
height=4cm,
keepaspectratio]{eps/pm-ok-2-1.png.eps}](img302.png)
![\includegraphics[%
width=1.0\columnwidth,
height=4cm,
keepaspectratio]{eps/pm-ok-2-2.png.eps}](img303.png)
![\includegraphics[%
width=1.0\columnwidth,
height=4cm,
keepaspectratio]{eps/pm-ok-2-3.png.eps}](img304.png)
![\includegraphics[%
width=0.23\columnwidth,
keepaspectratio]{eps/exp-calc-0.ppm.eps}](img309.png)
![\includegraphics[%
width=0.23\columnwidth,
keepaspectratio]{eps/exp-calc-2.ppm.eps}](img310.png)
![\includegraphics[%
width=0.23\columnwidth,
keepaspectratio]{eps/exp-calc-1.ppm.eps}](img311.png)
![\includegraphics[%
width=0.23\columnwidth,
keepaspectratio]{eps/exp-calc-3.ppm.eps}](img312.png)