Reconstruction de l'hémisphère

L'expression de la transformée de Fourier 2D discrète inverse est :

$$f(u,v)=\frac{1}{N^{2}}{\displaystyle \sum_{x=0}^{N-1}}{\displaystyle \sum_{y=0}^{N-1}}F(x,y).e^{\frac{2\pi j}{N}(xu+yv)}$$

Etant donné que nous travaillons sur un signal physique, nous devons extraire la partie réelle de la fonction complexe calculée avec la TFD inverse.

Soit :

$$H(x,y,u,v)=F(x,y).e^{\frac{2\pi j}{N}(xu+yv)}$$

et :

$$F(x,y)=q_{i}.e^{j\varphi_{i}}\textrm{, avec $i$\ l'indice de l'harmonique}$$

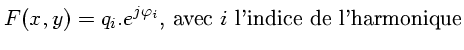
On a, avec $\Re$ représentant la partie réelle d'un complexe :

$$\Re[H] =\Re[q_{i}(\cos\varphi_{i}+j.\sin\varphi_{i}).(\cos\frac{2\pi}{N}(xu+yv)+j.\sin\frac{2\pi}{N}(xu+yv))]$$

$$=q_{i}(\cos\varphi_{i}\cos\frac{2\pi}{N}(xu+yv)-\sin\varphi_{i}\sin\frac{2\pi}{N}(xu+yv))$$

$$=q_{i}\cos(\varphi_{i}+\frac{2\pi}{N}(xu+yv))$$

d'où :

$$\Re[f(u,v)]=\frac{1}{N^{2}}{\displaystyle \sum_{x=0}^{N-1}}{\displaystyle \sum_{y=0}^{N-1}}q_{i}\cos(\varphi_{i}+\frac{2\pi}{N}(xu+yv))$$

Le signal discrétisé est reconstruit par B.1, soit :

$$\Re[f(\alpha,\beta)]=\frac{1}{N^{2}}{\displaystyle \sum_{x=0}^{N-1}}{\displaystyle \sum_{y=0}^{N-1}}q_{i}\cos(\varphi_{i}+x\alpha+y\beta)$$

Soit, avec les harmoniques choisis (B.2):

$$f(\alpha,\beta)=q_{0}+q_{1}\cos(\alpha+\varphi_{1})+q_{2}\cos(\be... ...i_{2})+q_{3}\cos(\alpha+\beta+\varphi_{3})+q_{4}\cos(-\alpha+\beta+\varphi_{4})$$