Structure des données
La structure de données représentant une texture directionnelle doit être choisie avec soin car nous avons deux contraintes : d'une part une texture directionnelle doit s'instancier très rapidement et d'autre part, elle doit occuper le moins d'espace mémoire possible.
Dans le premier cas, le point critique de l'instanciation est le calcul de localisation effectué en chaque texel lors du rendu (voir section 3.2.3). La structure, qui doit permettre des calculs rapides, est décrite en section 3.2.2.1.
Concernant la taille des données, nous décrivons en section 3.2.2.2 la méthode de quantifications des données que nous avons utilisée.
Discrétisation de l'hémisphère des directions
L'ensemble des directions utilisées pour le lancer de rayons est discrétisé
régulièrement en coordonnées sphériques. Cette discrétisation donne
un tableau de ![]() vecteurs distribués sur l'hémisphère. Les vecteurs
sont exprimés en coordonnées sphériques et répartis en
vecteurs distribués sur l'hémisphère. Les vecteurs
sont exprimés en coordonnées sphériques et répartis en
![]() tranches et
tranches et
![]() secteurs. Sur la figure 3.5,
secteurs. Sur la figure 3.5,
![]() et
et
![]() ; ce qui donne au total
; ce qui donne au total
![]() directions (la direction normale au texel n'est stockée qu'une seule
fois). Il y a donc
directions (la direction normale au texel n'est stockée qu'une seule
fois). Il y a donc
![]() azimuths, définis dans l'intervalle
azimuths, définis dans l'intervalle
![]() et
et
![]() angles polaires, définis dans l'intervalle
angles polaires, définis dans l'intervalle
![]() . Cette décomposition permet de retrouver
directement le secteur d'azimuth et d'angle polaire auquel appartient
une direction quelconque donnée.3.1
. Cette décomposition permet de retrouver
directement le secteur d'azimuth et d'angle polaire auquel appartient
une direction quelconque donnée.3.1
Quantifications
Afin de limiter la taille de la structure, l'ensemble des couleurs et l'ensemble des normales obtenues lors du lancer de rayons sont quantifiés de façon à être indexés. C'est à dire que pour chaque texel, dans une direction donnée, on ne stocke qu'un index vers la table des couleurs quantifiées et un index vers la table des normales quantifiées, ce qui réduit ainsi la taille de la structure (figure 3.6).
Couleurs
L'ensemble ![]() des couleurs à quantifier est obtenu lors du lancer
de rayons. Cet ensemble de couleurs est réduit à
des couleurs à quantifier est obtenu lors du lancer
de rayons. Cet ensemble de couleurs est réduit à ![]() couleurs distinctes
selon l'algorithme suivant :
couleurs distinctes
selon l'algorithme suivant :
- le tableau
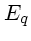 (de taille
(de taille 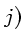 des couleurs quantifiées est
initialisé avec les
des couleurs quantifiées est
initialisé avec les 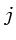 couleurs les plus représentées parmi
couleurs les plus représentées parmi 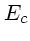 .
.
- pour les couleurs les moins représentées, on recherche la couleur
la plus proche (dans l'espace RVB) dans
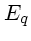 et on moyenne les
deux.
et on moyenne les
deux.
Normales
L'ensemble des normales est quantifié selon une méthode très simple : l'ensemble des directions de la sphère unité est discrétisé comme précédemment mais sur une sphère au lieu d'un hémisphère, puis on recherche pour chacune des normales la direction quantifiée la plus proche.
Distance
La distance ![]() (figure 3.4) entre le
point de la surface et le point d'intersection est utilisée lors du
calcul de l'éclairement. Cette valeur est exprimée par rapport à la
taille de la plus grande diagonale de la boîte englobante, qui correspond
à la valeur maximale possible.
(figure 3.4) entre le
point de la surface et le point d'intersection est utilisée lors du
calcul de l'éclairement. Cette valeur est exprimée par rapport à la
taille de la plus grande diagonale de la boîte englobante, qui correspond
à la valeur maximale possible. ![]() est donc exprimée comme proportion
de cette diagonale, et stockée sur un octet.
est donc exprimée comme proportion
de cette diagonale, et stockée sur un octet.
Finalement, nous obtenons pour chaque texel un tableau (d'orientations)
de taille ![]() stockant en chaque élément (figure 3.6)
:
stockant en chaque élément (figure 3.6)
:

Par exemple, pour une texture de définition 128x128 et un hémisphère composé de 500 directions, la structure occupe 31 Mo en mémoire, soit 128 Mo pour la totalité de la boîte.
Porquet Damien 2005-03-02
![\includegraphics[%
width=0.49\columnwidth,
keepaspectratio]{eps/discretisation_hemisphere.eps}](img351.png)
![\includegraphics[%
width=1.0\columnwidth,
keepaspectratio]{eps/tbp-precalc4.eps}](img352.png)