Liste des figures
- Le ''GMan'' du jeu vidéo Half-Life. A gauche, le modèle originel (environ 500 polygones, 1999), à droite le nouveau modèle (environ 5000 polygones, 2004)
- Simplification géométrique ([Hop96])
- Réduction d'arête et séparation de sommets
- Simplification avec préservation de l'apparence ([COM98]).
- Objet 3D représenté sous forme d'un nuage de points (sous échantillonné pour les mettre en évidence)
- Illustration d'un effet de parallaxe : la désocclusion. L'image de référence utilisée pour afficher la scène selon un autre point de vue ne contient pas assez d'informations et des trous apparaissent dans l'image à l'endroit ou on devrait voir une partie de la scène.
- Les deux principaux types d'images de profondeur. A gauche : carte d'élévations. A droite : carte de profondeurs issue de la projection de la scène sur le plan de projection d'une caméra.
- Les principales techniques de rendu à base de carte d'élévation ([WWT+03]).
- Calcul de l'auto-ombrage dans le relief induit
par une carte d'élévation selon Heidrich et al. [HS99].
Les points noirs correspondent aux vecteurs dont le rayon intersecte
le relief, tandis que les autres points représentent les directions
pour lesquelles la surface au point
 est visible. L'ensemble des
directions, contenues dans le cercle de rayon
est visible. L'ensemble des
directions, contenues dans le cercle de rayon
 (la base de l'hémisphère des directions), sont partitionnées par une
ellipse de rayons
(la base de l'hémisphère des directions), sont partitionnées par une
ellipse de rayons 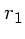 et
et  contenant les directions pour
lesquelles
contenant les directions pour
lesquelles  est visible. Les points extérieurs à l'ellipse et
contenus dans le cercle correspondent aux directions d'ombrage.
est visible. Les points extérieurs à l'ellipse et
contenus dans le cercle correspondent aux directions d'ombrage.
- Déplacement de surface dépendant du point de vue
- Définition d'une VDM ([WWT+03])
- Affichage par pixel de surface déplacée ([HEGD04]).
- Déplacement de surface basé image ([KS01])
- Déplacement de surface selon Schaufler ([SP99])
- Placage de texture en relief ([OBM00])
- Parallax Mapping
- Parallax mapping avec et sans décalage borné
- Placage d'environnement cubique
- Mélange d'images
- Pondérations utilisées dans [DTM96]
- Schémas de pondération de Pulli et al.
- View-Based Rendering.
- Horry et al. [HAA97]
- Décoret et al. [DDSD03]
- Yamazaki et al. [YSK+02]
- Imposteur. A gauche, l'objet original, à droite, l'imposteur.
- Imposteurs en couches ([Sch98])
- Imposteurs maillés de Sillion ([SDB97]).
- Principe de la rétroprojection de pixels
- 3D Image Warping
- Post-Rendering 3D Warping [MMB97]. Les zones noires des images correpondent aux trous dûs aux effets de parallaxe.
- Morphing [SD96]
- View morphing ([SD96])
- View Morphing de l'image
 vers l'image
vers l'image  . L'image intermédiaire
. L'image intermédiaire  est créée par
post-warping de l'image
est créée par
post-warping de l'image
 elle même obtenue
par transfert linéaire entre les images
elle même obtenue
par transfert linéaire entre les images
 et
et
 .
.
- Images à multiples centres de projection [RB98]
- Multiple Viewpoint Rendering [Hal98]
- Une tranche de lumière (Light-Slab) (à gauche) et ses deux plans positionnés dans l'espace de la scène (à droite).
- Acquisition des échantillons d'images de référence pour la construction d'un light-slab.
- Images panoramiques.
- Répartition des points de vue sur la sphère.
- Calcul de la contribution des points de vue de référence
- Exemples d'images de référence obtenues avec notre méthode
- Référentiel des images de référence
- Mélange pondéré de couleurs de trois points de vue de référence.
- Placage de texture dépendant du point de vue. Les trois points de vue de références utilisés sont éloignés les uns des autres d'un angle supérieur à 45^&cir#circ;. La figure du centre montre les effets de ghosting qui apparaissent (principalement autour du visage).
- Interpolation de deux points de
vue. A gauche, l'image de départ (
 . A droite, l'image d'arrivée
. A droite, l'image d'arrivée
 . A centre, le résultat de l'interpolation à
. A centre, le résultat de l'interpolation à  .
.
- Artefacts visuels lors du mélange d'images
- Ghosting. (a) : les trois points de vue de référence. (b), (c) et (d) : résultat de l'interpolation de textures selon différents angles, avec éclairage fixé.
- Texture de normales
- Placage de texture avec interpolation des normales pour le calcul de l'éclairement. Le maillage simplifié utilisé est composé de 3000 faces.
- Principe de l'interpolation de
points de vue : déplacement linéaire à l'écran des points de l'image
 de l'image de départ, à la position
de l'image de départ, à la position
 qu'il occupe selon le point de vue d'arrivée.
qu'il occupe selon le point de vue d'arrivée.
- Interpolation avec précalcul
du déplacement. Ligne supérieure : évolution des points du premier
point de vue. Ligne inférieure : évolution des points du second point
de vue. Colonne de gauche (pt. vue de départ) :
 , colonne
du milieu :
, colonne
du milieu :  , colonne de droite (pt. vue d'arrivée) :
, colonne de droite (pt. vue d'arrivée) :  .
.
- Interpolation avec précalcul du déplacement. En haut, sans filtrage bilinéaire. En bas, avec filtrage bilinéaire de l'image.
- Interpolation avec calcul au vol du déplacement des points.
- Principe de l'interpolation.
- Détermination du meilleur point de vue.
- Interpolation avec calcul ''au vol''
du déplacement dans les parties de superposant des images de référence.
De gauche à droite :
 ,
,  et
et 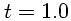 .
.
- Utilisation d'une boîte englobante pour résoudre le problème des points extérieurs à l'objet.
- Interpolation avec calcul ''au
vol'' du déplacement. De gauche à droite :
 ,
,  et
et
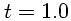 .
.
- Problème dus à l'interpolation linéaire
: dans les cas complexes, l'approximation par un segment de l'évolution
des points est impossible. En haut, les points de la scène balayés
par le rayon optique issu d'un pixel de la caméra virtuelle ; en bas
les points calculés. Les points rouges correspondent à
 et les
points verts à
et les
points verts à  Le modèle utilisé est le Dragon numérisé du
Laboratoire d'Informatique Graphique de Stanford.
Le modèle utilisé est le Dragon numérisé du
Laboratoire d'Informatique Graphique de Stanford.
- Maillage régulier.
- Déplacement des sommets du maillage de l'image de départ vers la position qu'ils occupent à l'écran selon le second point de vue.
- Attribution d'une profondeur virtuelle aux points extérieurs du maillage.
- Partitionnement de l'image en un nombre fixé de niveaux de profondeurs servant à la subdivision du maillage.
- Problème de la subdivision d'arête.
- Application de la subdivision d'arêtes avec prise en compte des T-vertices (image (a)). Les images (c) et (d) correspondent à la subdivision appliquée à l'ensemble de l'image plutôt qu'au maillage régulier (b).
- Comparaison des deux algorithmes de subdivision. A gauche, la première version générant des T-vertices. A droite, la version corrigée.
- Comparaison ne notre méthode avec le placage de texture dépendant du point de vue.
- Remplacement d'une partie de la scène par un polygone texturé (un imposteur).
- Précalcul : acquisition des informations géométriques pour chaque point des faces de la boîte englobante par lancer de rayons.
- Précalcul : lancer d'un rayon par
point, pour chaque direction
 de l'hémisphère.
de l'hémisphère.
- Discrétisation de l'hémisphère des directions.
- Quantification des normales et des couleurs.
- Rendu : reconstruction de la texture point par point en fonction des hémisphères précalculés stockant les intersections des rayons.
- Résultat de la méthode appliquée à un modèle de tore, en rendu à ombrage plat. La définition de la texture (figure (c) et (d)) est de 128x128 texels, l'hémisphère est constitué de 256 directions quantifiées. Temps de précalcul de 8 mn environ. Rendu à 15 FPS.
- Résultat de la méthode avec une boîte englobante complète. La définition des texture est 64x64 texels. La résolution de l'hémisphère est 250 directions.
- Création du nuage de points par subdivision récursive des triangles du maillage complexe.
- Résultat de notre méthode de discrétisation appliquée à un tore à surface perturbée avec une carte d'élévation (par déplacement de surface) et à un maillage représentant un noeud torique.
- Calcul d'une texture directionnelle
- Variation de l'échantillonnage de la surface de la scène, avec des rayons issus de l'hémisphère des directions d'un texel de la boîte englobante.
- Répartition adaptée des directions sur l'hémisphère. La répartition de l'angle d'élévation est basée sur une portion de la fonction racine carrée et permet d'augmenter le nombre de directions aux angles rasants.
- Construction du repère
local d'un point. - BRDF par acquisition physique.
- Résultats pour une variation de l'éclairement (de haut en bas). Définition des textures : 128x128 ; 1742 directions ; QLS : 4.97 Mo ; Hémisphères de visibilité : 326.81 Mo. Colonnes de gauche à droite : Phong (20 FPS), BRDF de Satin (15 FPS), BRDF synthétique (15 FPS). Toutes les images emploient l'auto-ombrage.
- Méthode appliquée à un modèle composé
de petits objets : le dirigeable, ligne du haut. Définition des textures
: 64x64, Nb. directions : 4902, 50 FPS, pas de d'interpolation bilinéaire.
Ligne du bas : résultat de la méthode appliquée au tore pour différentes
définition de texture : 128
 (20 FPS), 64
(20 FPS), 64 (50 FPS) et 32
(50 FPS) et 32 (70 FPS) de gauche à droite.
(70 FPS) de gauche à droite.
- Modèles d'illuminations gérés par notre méthode. La définition des textures utilisées pour ces images est 128x128. Pour une qualité d'image maximale, nous avons positionné l'observateur à un pôle de l'hémisphère. De gauche à droite : Phong, Phong+placage d'environnement, BRDF satin, BRDF synthétique.
- Application de l'auto-ombrage
par compression en harmoniques principaux de l'hémisphère d'ombrage.
Images de gauche : rendu standard (Phong) 30 FPS. Images de droite
: application de l'auto-ombrage, 20 FPS. Le segment blanc indique
la direction de l'éclairage. Définition de texture 128
 .
.
- Trajectoire de la caméra.
- Segmentation de la variation de profondeur d'un pixel de l'écran. Abscisses : abscisse curviligne de la caméra sur la trajectoire. Ordonnées : profondeur du pixel.
- Principe de la reconstruction de la surface.
- Disparités de profondeur.
- Origine des points utilisés pour reconstruitre les pixels de l'image.
- Résultats de l'interpolation.
- Comparaisons de la méthode avec différentes compressions.
- Application de la méthode au modèle Armadillo, compression sur 10 segments. Ligne du haut : interpolation à différentes position de la trajectoire. Ligne du bas : variation de la position de l'éclairage.
- Acquisition des points de vue de référence.
- Principe du placage de géométrie sur le modèle simplifié.
- Application de notre méthode d'interpolation de points de vue au modèle du Buddha, composé de 1.1 million de faces.
- A gauche, résultats de la méthode avec différents modèles simplifiés. A doite, application de la méthode au modèle de dragon. En bas à droite, vue détaillée de l'application de l'auto-ombrage.
- Améliorations. Plutôt que de reprojeter
un à un les points affichés d'un triangle
 du maillage simplifié
(en gris) sur chaque point de vue de référence, nous pourrions obtenir
ces points directement en pré-projetant
du maillage simplifié
(en gris) sur chaque point de vue de référence, nous pourrions obtenir
ces points directement en pré-projetant  dans les images de référence.
dans les images de référence.
- Echantillonnage d'un rayon optique
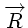 .
.
 = le point que nous utilisons actuellement pour afficher
= le point que nous utilisons actuellement pour afficher
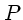 .
.  = le point réel de la surface du maillage complexe de
base. L'idée est de converger vers
= le point réel de la surface du maillage complexe de
base. L'idée est de converger vers  par échantillonnage de
par échantillonnage de
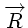 à partir du point
à partir du point 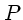 .
.
- Vertex Shader
- Pixel Shader
- Unité de rastérisation
- Hémisphère d'ombrage.
Porquet Damien 2005-03-02